Wolfram|Alpha 是非常好用的计算器,可用来求解一阶、二阶和三阶导数、在某个点的导数以及偏导数。帮助您理解什么是导数,同时为您展示 Wolfram|Alpha 如何计算导数。
WolframAlpha
在线导数计算器
用 Wolfram|Alpha 求导数
卓越的在线导数计算器
进一步了解
输入查询的小窍门
用普通英文输入查询。为避免引起歧义,在必要时请使用括号。下面的例子将向您展示如何输入求导的查询。
访问快速学习工具
通过分步解答和 Wolfram 习题生成器获取及时反馈和指导。
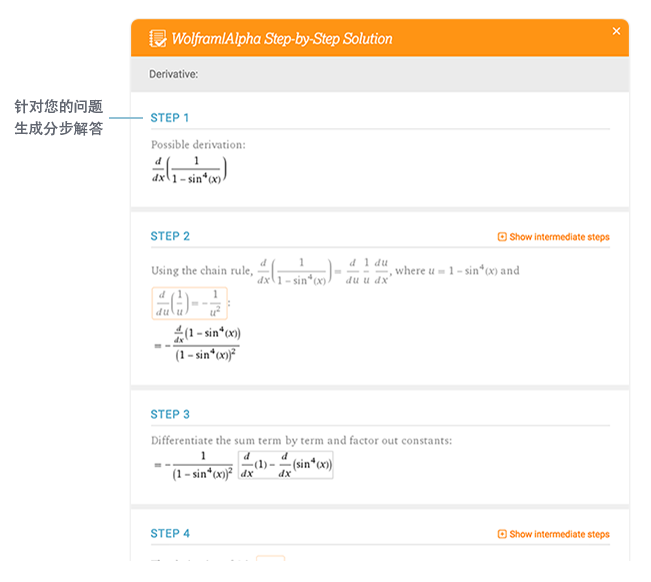
进一步了解
什么是导数?
导数是微积分学中的一个重要工具,它表示的是函数关于自身某个变量的无限小的变化率。
对于函数 f x,有很多种方法可用来表示 f 关于 x 的导数。其中,最常见的是 d fd x 和 f'x。对于 n 次求导,可用 dn fdxn 或 fnx 来表示。我们称其为高阶导数。而对于二阶导数,则经常用记号 f''x 来表示。
在点 x = a 处的导数被定义为 f'a = limh0f a + h - f hh 。该极限不一定存在,但是,如果存在,则可以说 f x 在 x = a 处可导。从几何学上来看,f'a 是 f x 在 x = a 处切线的斜率。
我们来看一个范例,如果 f x = x3,则 f'x = limh0h+x3-x3h = 3x2 再来计算 f''x:f''x = limh03x+h2-3 x2h = 6x。我们可以将导数这个强大工具应用到很多方面。例如,求局部/全局极值、求拐点、解决优化问题以及描述物体的运动。
Wolfram|Alpha 如何计算导数
Wolfram|Alpha 调用 Mathematica 内的 D 函数,该函数使用一个恒等式表,这个表比一般微积分教科书中的要大的多。其中包括很多“众所周知”的法则,比如求导的线性性、乘积法则、幂函数求导法则、链导法则等等。此外,D 还使用一些“不知名”的法则来计算大量特殊函数的导数。对于高阶导数,则使用类似于广义莱布尼茨乘积法则的规则来加快计算速度。