Wolfram|Alpha 是一款优秀的计算工具,可用来计算反导数和定积分、双重和三重积分以及反常积分。通过显示绘图、替代形式和其他相关信息提高你的数学直觉思维能力。
在线积分计算器
用 Wolfram|Alpha 求积分
卓越的在线积分计算器
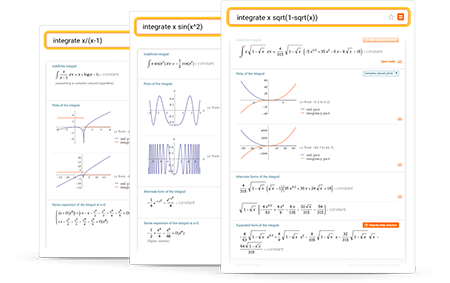
进一步了解
输入查询的小窍门
用普通英文输入查询。为避免引起歧义,在必要时请使用括号。下面的例子将向您展示如何输入求积分的查询。
访问快速学习工具
通过分步解答和 Wolfram 习题产生器获取及时反馈和指导。
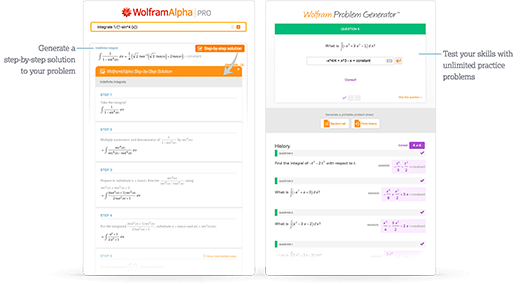
进一步了解
什么是积分?
积分是微积分学中的一个重要工具,它可以给出反导数或表示曲线下的面积。
我们将 f(x) 的不定积分表示成 ∫f(x) dx,它被定义为 f(x) 的反导数。换句话说,∫f(x) dx 的导数是 f(x)。由于常数的导数是零,不定积分只能定义到任意常数。例如,∫sin(x) dx=−cos(x)+常数,因为 −cos(x)+常数 的导数是 sin(x)。我们将 f(x) 从 x=a 到 x=b 的定积分表示成 ∫baf(x) dx,它被定义为 f(x) 和 x 轴 之间从 x=a 到 x=b 的有符号的面积。
两种类型的积分由微积分学的基本原理联系在一起。这表明如果 f(x) 在区间 [a,b] 上可积并且 F(x) 是它的连续不定积分,则有 ∫baf(x) dx=F(b)−F(a)。 这意味着 ∫π0sin(x) dx=(−cos(π))−(−cos(0))=2。有时我们想要求一个定积分的近似值,常见的方法为在曲线下放置细的矩形,并将这些有符号的面积加在一起。Wolfram|Alpha 能求解各种各样的积分。
Wolfram|Alpha 是怎样计算积分的
Wolfram|Alpha 计算积分的方法和我们人类手动计算的方法不一样。它通过调用 Mathematica 内的积分函数来实现,这表示涉及了巨量的数学和计算研究工作。它完成积分的方法和人类完全不同。它采用了非常强大、通用的算法,其中包含了异常复杂的数学原理。有几种常用的方法。其中之一为先将积分转换为通用形式,再取微分并通过解方程确定未知的符号参数。有时,被积函数非常简单,但为此产生的方程却极为复杂,需要运用 Mathematica 强大的代数运算能力来解决。Mathematica 使用的另一种方法是将被积函数转换成广义超几何函数,然后再对这些数学函数运用关系式。
尽管这些强大的算法使得 Wolfram|Alpha 具有了快速计算积分和处理大量特殊函数的能力,理解人类计算积分的方法同样重要。因此,Wolfram|Alpha 也包含了分步计算积分的算法。这些算法使用了完全不同的积分技巧,模仿的是人类计算积分的思路和方法。其中包括换元积分法、分部积分法、三角换元法及部分分式积分法。