Wolfram|Alpha 是求多项式的根和解方程组的绝佳工具. 它还可以对多项式进行因式分解、绘制多项式的解集和不等式的图形等。
在线方程求解器
用 Wolfram|Alpha 求解线性、二次以及多项式方程组
不仅仅是一个在线方程求解器
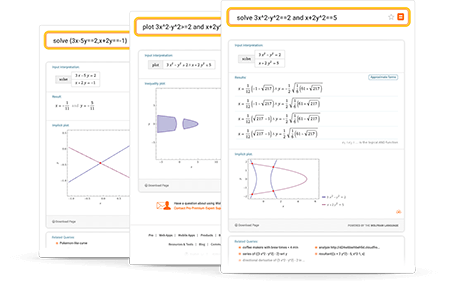
进一步了解
输入查询的小窍门
使用简洁语言进行查询。为避免出现模棱两可的查询,必要时请使用括号。下面是一些范例,说明应该怎样构建合理的查询。
访问快速学习工具
通过分步解答和 Wolfram 习题生成器获取及时反馈和指导。
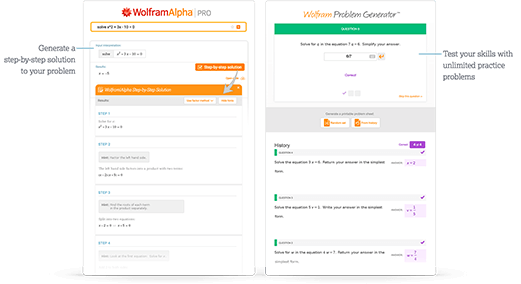
进一步了解
关于求解方程
如果 pc=0,则称值 c 为多项式 px 的根。
出现在 px 中的 x 的最大指数称为 p 的次数。如果 px 的次数为 n,那么众所周知,如果将多重根考虑在内,就存在 n 个根。为理解多重根的含义,我们来看 x2 - 6x + 9=x-32=x-3x-3 这个例子。这个多项式被认为有两个根,都等于 3。
人们通常是在代数的第二门课程中学习“因式定理”,作为找到所有有理数根的一种方法。人们还会学习如何找到所有二次多项式的根,必要时使用平方根(由判别式产生)。有更高级的公式用于表示三次多项式和四次多项式的根,还有许多用于近似任意多项式根的数值方法。这些要用到复分析以及复杂的数值算法,事实上,这个领域的研究和发展还在持续进行。
人们通常使用高斯消元法或相关方法求解线性方程组。通常在中学或大学数学课程中遇到,需要更高级的方法来求非线性联立方程组的根。类似的结论也适用于不等式方程组:可以使用线性代数课程中介绍的方法处理线性方程组,对于更高次的多项式方程组,通常需要更复杂的计算工具。
Wolfram|Alpha 如何求解方程
求解方程时,Wolfram|Alpha 调用 Wolfram 语言的 Solve 和 Reduce 函数,其中包含各种代数方法,从基本的线性和二次方程到多元非线性方程组,都可求解。在某些情况下,会用到诸如高斯消元法的线性代数方法,并进行优化以提高速度和可靠性。其他运算需要数论、抽象代数和其他高等领域的定理和算法来计算结果。这些方法经过精心设计和选择,以支持 Wolfram|Alpha 最大限度地解决各种问题,同时尽可能地减少计算时间。
尽管这些方法对于直接获得解很有用,但对于系统来说,了解人类如何解决相同的问题也很重要。因此,Wolfram|Alpha 还另行提供通过人类易于识别和使用的传统技巧来求解的方法,并分步展示代数运算。这包括消元法、代入法、二次方程求根公式、克莱姆规则等等。