Wolfram|Alpha 能够求解各种方程组。它可以求解线性方程组或涉及非线性方程的方程组,还可以专门求整数解或其他定义域的解。此外,它还能求解涉及不等式和更多一般约束条件的方程组。
WolframAlpha
在线 方程组求解器
用 Wolfram|Alpha 求解方程和方程组
求解方程组和约束条件的强大工具
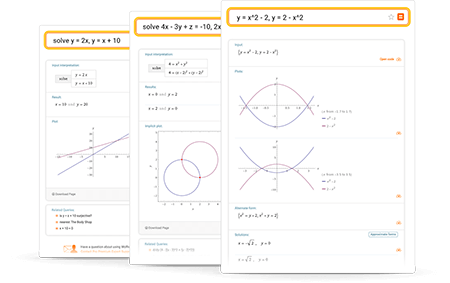
进一步了解
输入查询的小窍门
使用简洁语言进行查询。为避免出现模棱两可的查询,必要时请使用括号。下面是一些范例,说明应该怎样输入合理的求解方程组的查询。
访问快速学习工具
通过分步解答和 Wolfram 习题生成器获取及时反馈和指导。
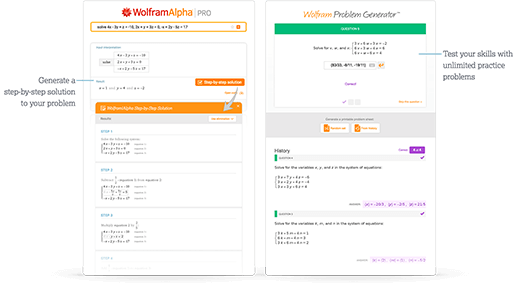
进一步了解
什么是方程组?
方程组是涉及多个变量的一个或多个方程。
方程组的解是使所有方程都满足要求的变量映射,换句话说,就是所有方程组的交点。求解一个方程组就是找到所有这样的公共解或交点。
线性方程组是方程组的一个常见且适用的子集。在两个变量的情况下,方程组可以被看作是在二维空间中绘制的线条。如果所有的线都汇聚到一个点,则称该方程组是相容的,在这个交点上有一个解。反之,则方程组是不相容的,没有解。涉及两个以上变量的线性方程组的情况类似,要么只有一个解,要么无解,要么有无限多个解(后者是指所有方程都等价的情况)。
涉及非线性函数的更广义的方程组也是可能的。这些方程组拥有更复杂的解集,涉及一个、零个、无限或任意数量的解,但其工作原理与线性方程组类似,其解是满足所有相关方程的点。此外,还可能出现更多有一般约束条件的方程组,例如涉及不等式或要求某些变量为整数的约束条件。
解方程组是一个非常普遍和重要的概念,是数学、工程学和科学等许多领域的基础概念。